“Binary search” is a computer science term used in programming and software engineering. It is a way of determining if a value exists in an ordered data set. It’s considered a textbook algorithm. It is useful because it reduces the search space by half on each iteration.
Imagine we are asked to search for an integer in an array that is sorted in ascending order. The challenge is to return the target number’s index.
We could use a built in JavaScript function indexOf():
var search = function(nums, target) {
var answer = nums.indexOf(target);
console.log(answer);
return answer;
};
console.log(search([-1,0,3,4,5,9,12], 5)); // returns '4'
But that is an abstraction, which can be slow and expensive. Instead, we should implement our own binary search code.
Binary Search Implementation
Binary search starts in the middle of a collection, and checks if that is the requested term. The initial middle position is determined by taking the length of the array and dividing it by two. If the array has an even number of elements, then the ‘halfway position’ is considered close enough. I use a JavaScript Math function to round down, making sure I am not left with a decimal floating number:
cursor = Math.floor( ((left + right) / 2) ); // about the middle
If the search term is not found, the position (the cursor) is moved. Since the collection is ordered from smallest to largest we know which direction to move the search cursor. If the target is less than the current value, we shift one to the left. If the target is greater than the current value, we shift two to the right.
This continues until the target query is found. That sequence is ran inside of a loop. The loop repeats while the left boundary is less than (or equal to) the right. The search cursor’s index is changed by adjusting the left or right bounds. Once adjusted, the cursor is recalculated on the subsequent iteration.
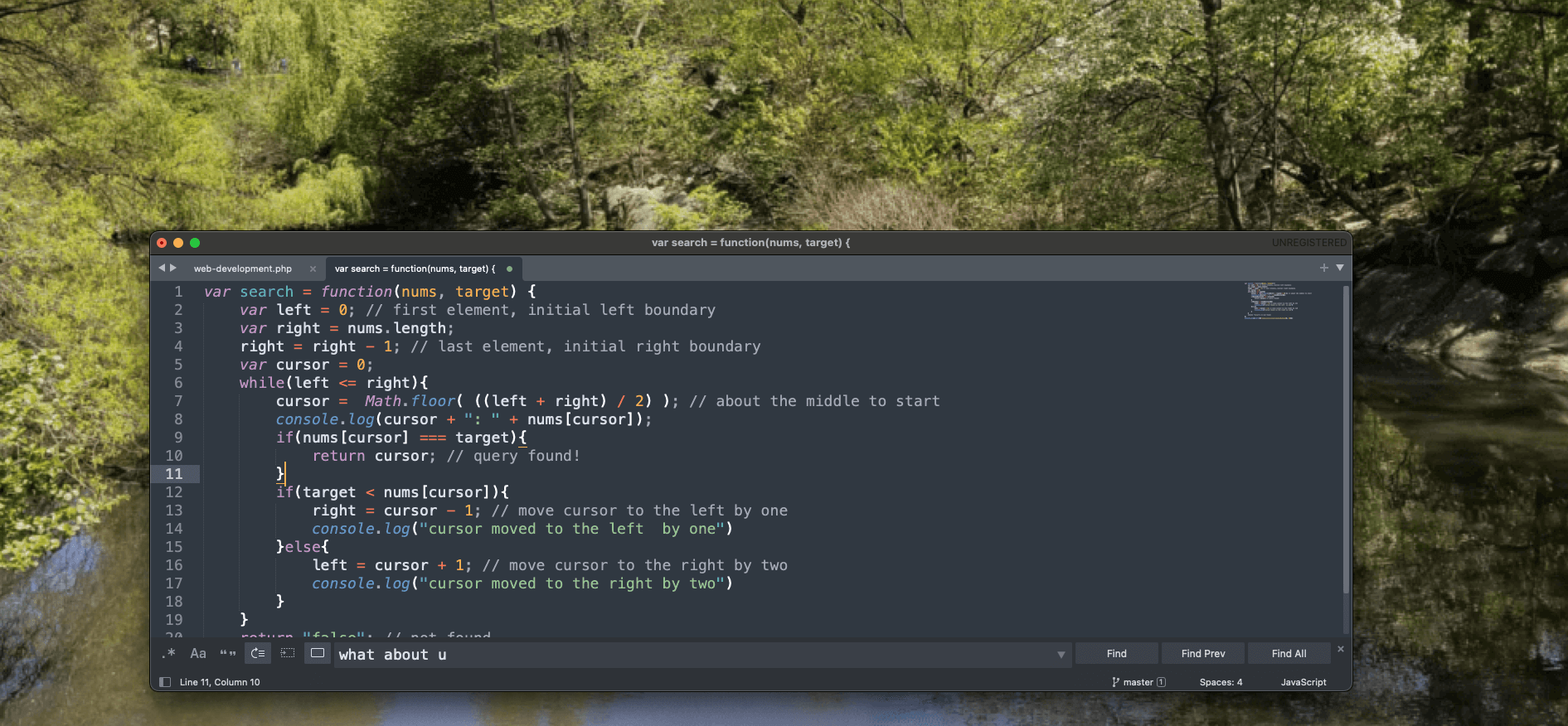
var search = function(nums, target) {
var left = 0; // first element, initial left boundary
var right = nums.length;
right = right - 1; // last element, initial right boundary
var cursor = 0;
while(left <= right){
cursor = Math.floor( ((left + right) / 2) ); // about the middle to start
console.log(cursor + ": " + nums[cursor]);
if(nums[cursor] === target){
return cursor; // query found!
}
if(target < nums[cursor]){
right = cursor - 1; // move cursor to the left by one
console.log("cursor moved to the left by one")
}else{
left = cursor + 1; // move cursor to the right by two
console.log("cursor moved to the right by two")
}
}
return "false"; // not found
};
console.log(search([-1,0,1,2,3,4,5,6,7,8,9,10,11,12], 10));
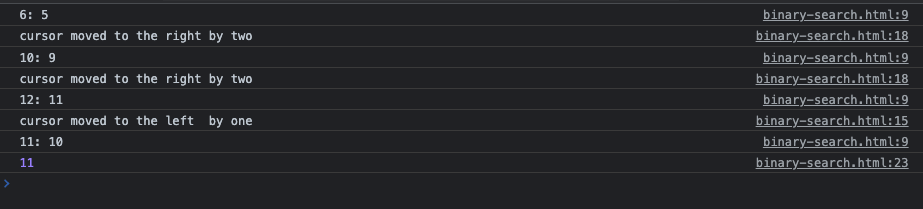
The above code starts to search in the central location, nums[6] == 5. Look at the output below to see how the cursor moves until it finds the target value of 10 (at a zero-based index of 11):
This algorithm has an O(log n) runtime complexity. That Big-O notation describes how it would scale as the input increases. Imagine an array with thousands of elements. O(log n) means that the time to execute this code will increase linearly only as the number of input items increase exponentially. That means our code is performant and efficient.
Square root algorithm using binary search
Another implementation example of using binary search in a JavaScript function is to calculate the square root of a number. Now, of course, Javascript has a built in Math.sqrt() function that is highly performant compared to any custom code we will write. But, it is a good exercise to think about how this works.
The square root of a number is a value that, when multiplied by itself, gives the original number. To solve for it when given an input, we are going to take a guess at what the answer (square root) is, starting with itself divided by two (giving us the midpoint between it and zero). We multiply that midpoint by itself to check our guess. It will only be correct on the first iteration if the input is the number four (four divided by two is two; two times two is four). Otherwise, we will move the cursor (halving the search range) to either the left or the right, depending on if the square of our guess is larger or smaller than the original input.
The concept of “moving the cursor” helps to visualize how the binary search algorithm zeroes in on the square root by iteratively narrowing down the search range based on the comparison of the square of the midpoint to the target number.
I accounted for two special cases in my code. For negative numbers we return false because negative numbers have imaginary square roots. For numbers smaller than one we set the range’s end to one because the square root of a fraction is larger than the fraction itself. Additionally, I set a precision threshold (0.0000000001), because some numbers have square roots that are irrational.
function binarySearchSquareRoot(n, precision = 1e-10) {
if (n < 0) {
throw new Error('Input must be a non-negative number');
}
let start = 0;
let end = n;
// If the number is less than 1, set end to 1 to handle fractions
if (n < 1) {
end = 1;
}
while (end - start > precision) {
const mid = (start + end) / 2;
const midSquared = mid * mid;
if (midSquared === n) {
return mid; // Found exact square root
} else if (midSquared < n) {
start = mid;
} else {
end = mid;
}
}
return (start + end) / 2; // Return approximate square root
}
// Usage:
const number = 25;
const squareRoot = binarySearchSquareRoot(number);
console.log(`The square root of ${number} is approximately ${squareRoot}`);
Alternatively, the Babylonian algorithm can be implemented to solve for square roots.