During my early twenties, I was working as a pizza delivery driver, and with an opportunity to shape my future. While cruising through the city streets, I knew that I wanted more from life and was determined to seize every spare moment to pursue my passion for knowledge. With the help of audio books and programs I discovered on the internet, I embarked on a journey of self-education. Fueling my curiosity, I delved into the world of self-improvement, philosophy, and personal power. I became inspired to work for myself, and decided to pursue a career in professional web development.
Years later, the pizzeria where I once worked commissioned me to build their website. In a strange way, it was a moment of validation, showcasing how far I had come since my days behind the wheel.
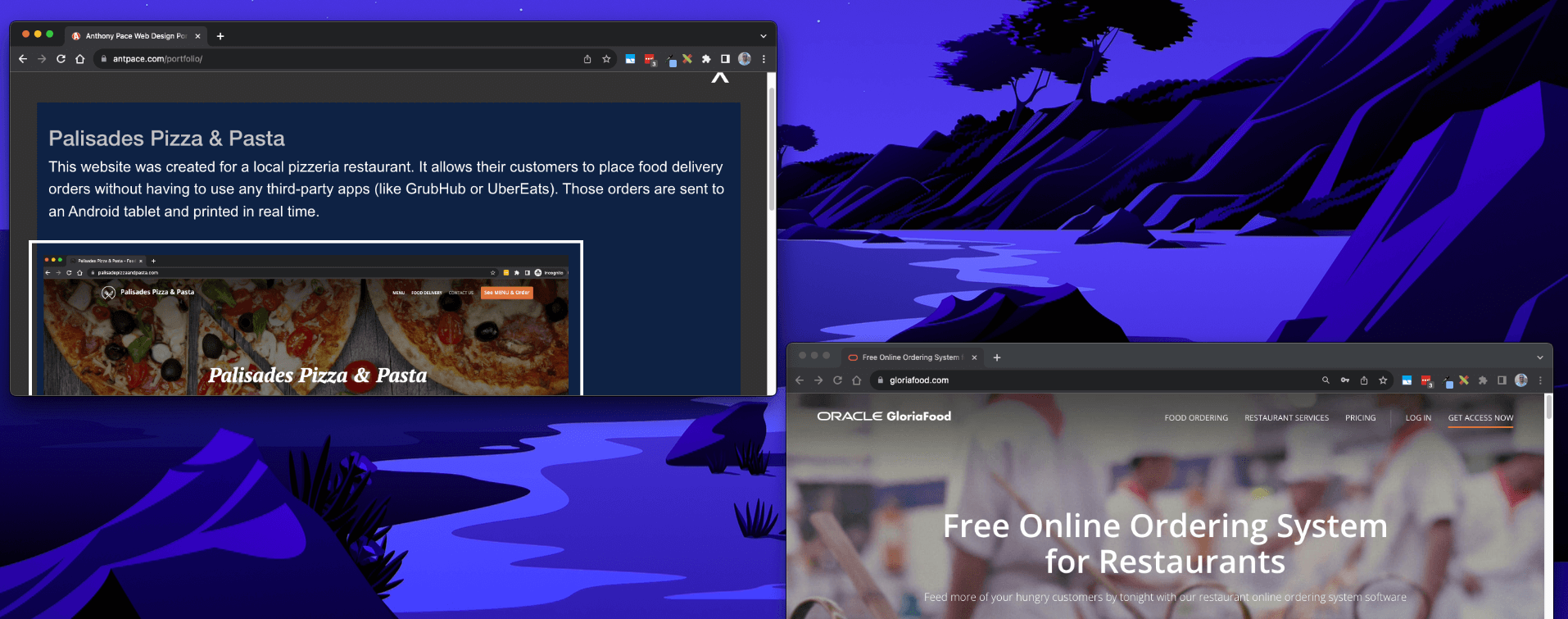
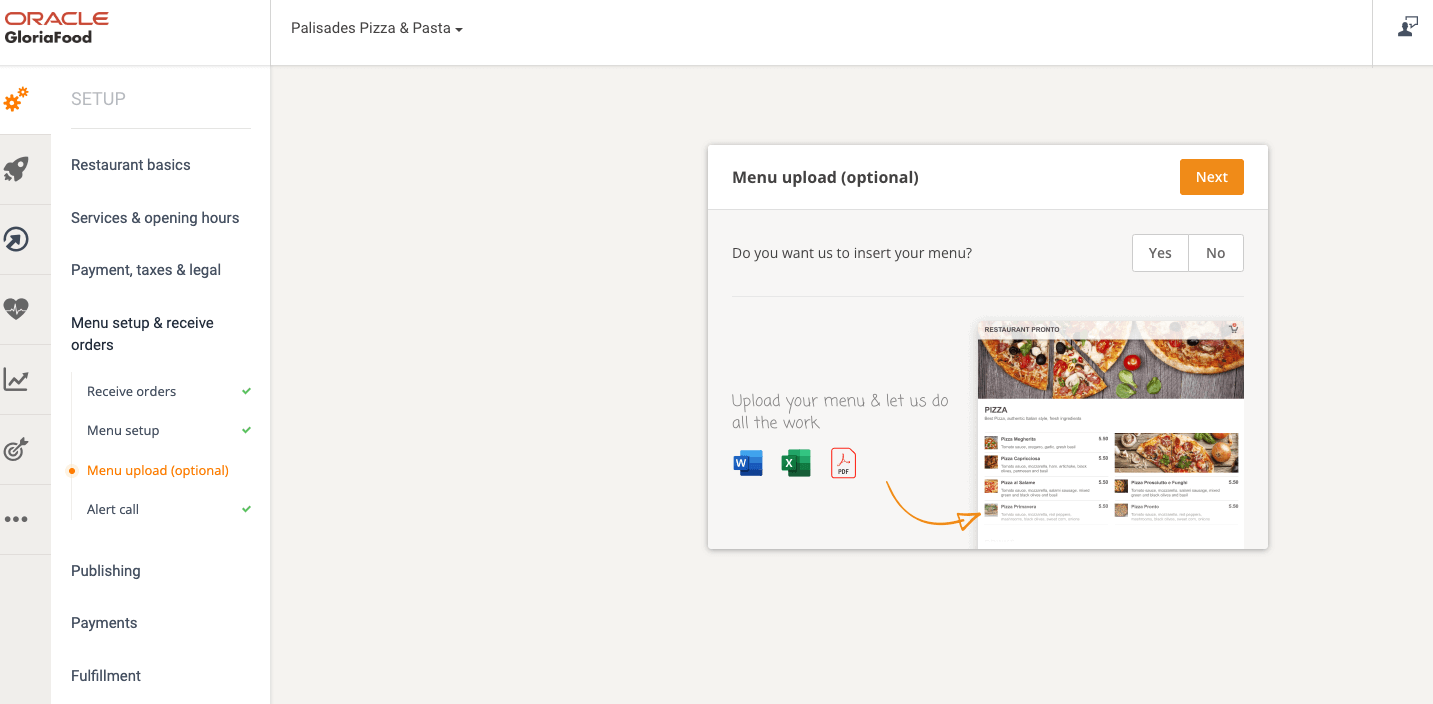
The pizzeria wanted their website to be able to take orders for food online and send a notification to their iPad. By doing this, they could avoid using apps like GrubHub that charged additional fees. To make this happen, I used a service called GloriaFood that provided ready-made website templates, a secure payment process, and a messaging system. It integrates with Stripe for processing payments. There is an iPad app that receives push notifications when new orders are placed. The website builder required no code, and had a ton of options. I was able to register the pizzeria’s domain name directly though the admin portal, and generate a sales optimized website with hosting all setup. It was “seamless” – pun intended!
There are also options for integrating their ordering UI with an existing website, a Facebook page, or a dine-in QR code. The an option to publish a custom app required an additional cost per month.
I even traveled to this restaurant’s physical location, selected and purchased a tablet computer for them, installed the GloriaFood app to receive orders, and connected it to their mobile printer.
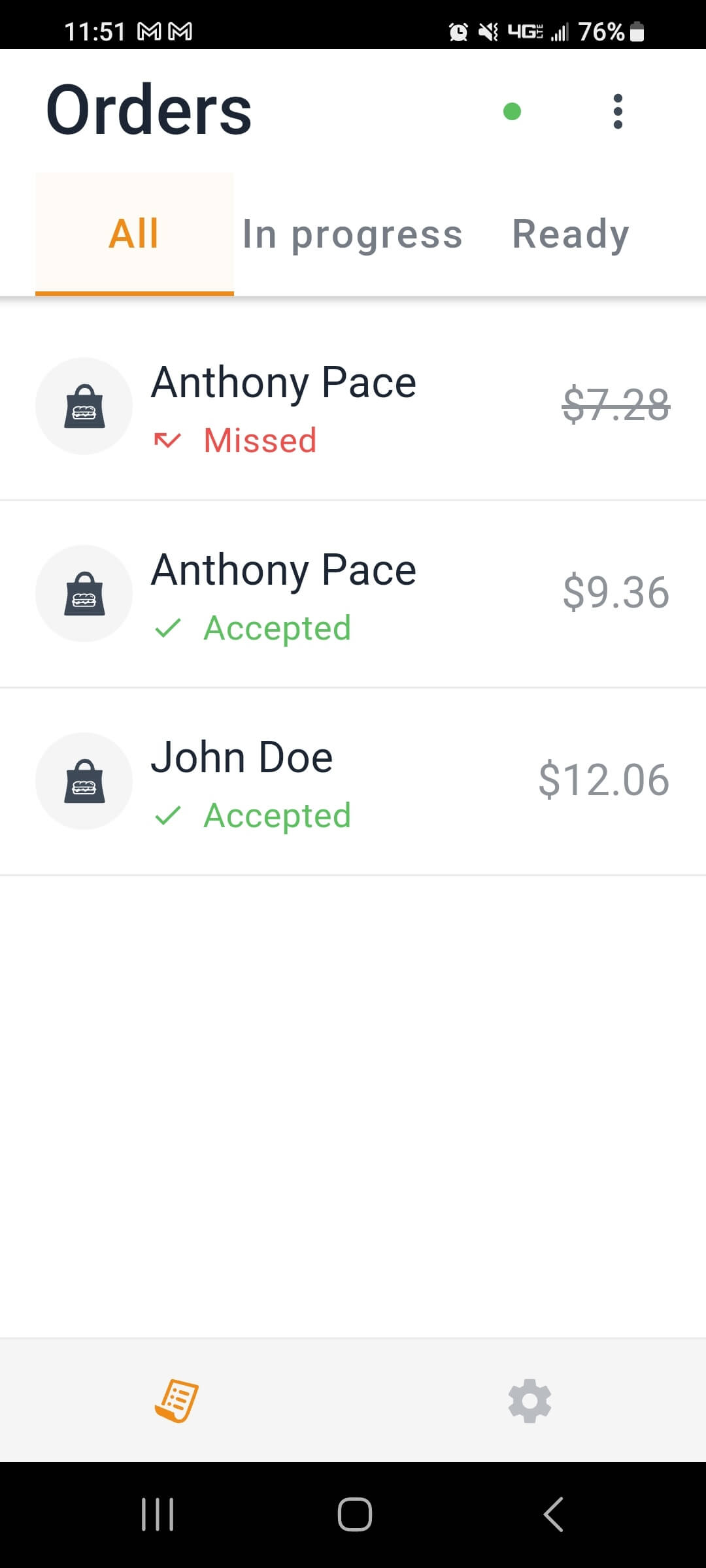
It’s amazing how much I was able to accomplish without writing a single line of code. The most technical part of this project was setting up a Stripe account and putting the API keys into the GloriaFood admin panel. GloriaFood is a product by Oracle, a company that specializes in providing a wide range of software and hardware products and services.
As an extra part of this project, I designed a business card with a QR code linking to the new website. The business owner planned to give this to customers who ordered through other food ordering apps such as GrubHub, Seamless, UberEats, and Slice.
