A common coding challenge that you may encounter will ask you to write a function that returns the Fibonacci sequence, up to the nth number (which is provided as an argument). Below is a solution, along with some commentary about the topic. This challenge is a great exercise in problem solving.

Fibonacci numbers
The sequence starts with 0 and 1, and the next number in the sequence is always the sum of the previous two numbers. The first few terms of the sequence are:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811
Since this series follows a known pattern, we can write code to generate it up to a specified position.
In mathematics, the Fibonacci sequence is a sequence in which each number is the sum of the two preceding ones. Numbers that are part of the Fibonacci sequence are known as Fibonacci numbers.
These numbers were first described in ancient Indian mathematics. They are named after the Italian mathematician Leonardo of Pisa, also known as Fibonacci, who introduced the sequence to Western European mathematics in his 1202 book Liber Abaci. Fibonacci numbers are also strongly related to the golden ratio. In computer science, these numbers can be applied to programming algorithms related to search, data structures, and graphs.
Recursion
In programming, recursion is an important concept. Recursion is when a function calls itself. Writing code that generates the Fibonacci sequence requires recursion. Here is an example in JavaScript:
function fibonacci(n) {
if (n < 2){
return 1;
}else{
return fibonacci(n-2) + fibonacci(n-1);
}
}
console.log(fibonacci(7)); // Returns 21
If you ask this function for 0 or 1 terms, it will simply return 1. It is the condition that will ultimately stop the recursion. Anything above that, it will have to call itself recursively. What exactly is happening there? This Stack Overflow thread does a great job stepping though the logic and illustrating each iteration.

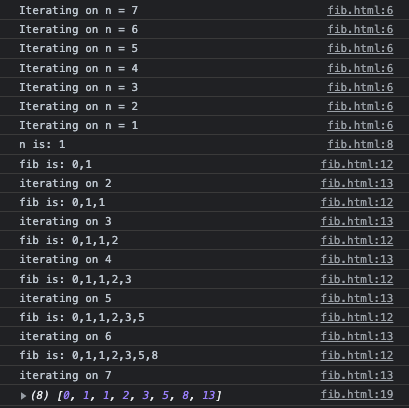
When I decorate the code from above with console log statements and collect the results into an array, it becomes obvious:
function fibonacci(n) {
console.log("Iterating on n = " + n)
if (n <= 1) {
console.log("n is: "+n)
return [0, 1].slice(0, n + 1);
} else {
const fib = fibonacci(n - 1);
console.log("fib is: "+fib)
console.log("iterating on " + n)
fib.push(fib[fib.length - 1] + fib[fib.length - 2]);
return fib;
}
}
You can see it iterates all the way down, starting at the desired argument of term numbers, and ending with 1. Once it gets to the bottom, it starts going back up. On each subsequent round, it adds a new number to the result array by summing the previous two numbers.
I asked ChatGPT to rewrite this code for me, and this is how it was cleaned up:
function fibonacci(n) {
if (n <= 1) {
return [0, 1].slice(0, n + 1);
} else {
var sequence = fibonacci(n - 1);
sequence.push(sequence[sequence.length - 1] + sequence[sequence.length - 2]);
return sequence;
}
}
This function has an exponential time complexity. It can be very slow for larger values of n.
Memoization and Cacheing
This challenge is often followed with a request to make it “more performant”. I mentioned above that our solution has “exponential time complexity”. Its algorithmic efficiency can be described as O(2^n) in Big O notation.

Every call (while n is greater than 1) results in two additional recursive calls, one with n-1 and another with n-2. Each of those calls then results in two more recursive calls, and so on, resulting in a binary tree of recursive calls.
The performance of this code can be improved by implementing memoization. Memoization is when we store the results of our function call. On subsequent calls, our application can look up answers it previously calculated without have to do the work again.
function fibonacci2(n, memo = {}) {
if (n in memo) {
console.log("we used the memo on: " + n)
return memo[n];
}
if (n <= 1) {
return [0, 1].slice(0, n + 1);
} else {
const fib = fibonacci2(n - 1, memo);
fib.push(fib[fib.length - 1] + fib[fib.length - 2]);
memo[n] = fib;
return fib;
}
}
memo = {}
console.log(fibonacci2(7, memo));
console.log(fibonacci2(15, memo));
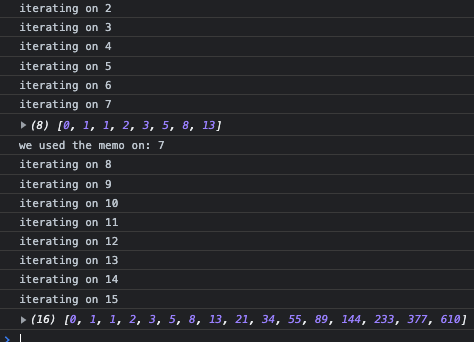
On each iteration we save the results to an array called memo. When we use the function, we first check to see if the answer we want is already stored in our cache. Our course, the work still needs to be done the first time around, but never again – making computation much faster in the future. You can see that my 2nd call can start where the results of the previous call left off:
By using memoization, this implementation of the Fibonacci function has a time complexity of O(n). Another way to improve the performance of our code, without using memoization, is to use a loop:
function fibonacci(n) {
var sequence = [0, 1];
for (var i = 2; i <= n; i++) {
sequence.push(sequence[i-1] + sequence[i-2]);
}
return sequence;
}
The choice between memoization or a loop depends on the specific requirements and constraints of the use-case. While the time complexity of a loop-based solution is still O(n), it can be faster than the memoization approach for small or medium-sized values of n. If simplicity and readability are a higher priority, or if memory usage is a concern, a loop-based solution may be a better option.
Memoization is considered a “dynamic programming” technique. Dynamic programming involves solving sub-problems once and storing the results for future reference, which can significantly improve the efficiency of the overall solution.